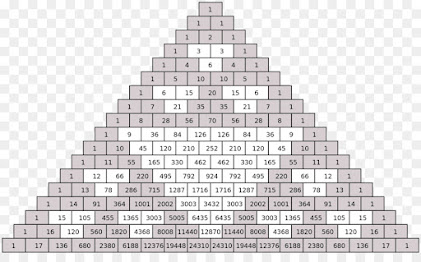
ТРЕУГОЛЬНИК ПАСКАЛЯ

Треугольником Паскаля - бесконечная таблица в форме треугольника, в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел. Получил название в честь великого французского математика Блеза Паскаля.

Чтобы обнаружить арифметическую прогрессию чисел высших порядков необходимо провести диагональ, как показано на рисунке ниже. 

Рассмотрим последовательность на 10 строке. Там располагаются числа 1,9,36, 84,126,126,84,36,9,1. От 1 до 5 числа прогрессия у нас возрастает, а с 6 по 10 уменьшается. Замечаем, что тут аж 2 прогрессии, и убывающая, и возрастающая. И так с каждой строкой этого Бесконечного Треугольника. Это мы рассмотрели прогрессию по строке Треугольника. А теперь мы посмотрим по диагонали. Обращается снова к нашему рисунку. На диагонали расположены числа 1,9,45,165. Это арифметическая прогрессия 8 порядка.





  



  

Комментарии

Отправить комментарий

Популярные сообщения из этого блога

1.Иога́нн Карл Фри́дрих-  немецкий   математик ,  механик ,  физик ,  астроном  и  геодезист . Считается одним из величайших математиков всех времён, «королём математиков» .   Карл Гаусс сделал фундаментальные открытия почти во всех областях алгебры и геометрии. Самым плодотворным периодом считается время его обучения в Гёттингенском университете. Находясь в коллегиальном колледже он доказал закон взаимности квадратичных вычетов. А в университете математик сумел построить правильный семнадцатиугольник с помощью линейки и циркуля и решил проблему построения правильных многоугольников. Этим достижением ученый дорожил больше всего. Настолько, что пожелал выгравировать на его посмертном памятнике круг, в котором бы находилась фигура с 17 углами. В 1801 году Клаус издает труд «Арифметические исследования». Через 30 лет на свет появится очередной шедевр немецкого математика – «Теория биквадратичных вычетов». В нем приводятся доказательства важных арифме...
Далее...
Изображение
   Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвёртый больше третьего и пятый больше четвертого. Кроме того, двое первых должны получить в 7 раз меньше трёх остальных. Сколько нужно дать каждому? Решение  Пусть у- разность арифметической прогрессии, тогда  доля первого – х; доля второго – (х + у);  доля третьего – (х + 2у); доля четвертого – ( х + 3у); доля пятого – (х + 4у).  Затем составим систему уравнений: Задача  За 16 дней Карл украл у Клары 472 коралла. Каждый день он крал на 3 коралла больше, чем в предыдущий день. Сколько кораллов украл Карл в последний день? Задача  В амфитеатре расположены 10 рядов, причем в каждом следующем ряду на 20 мест больше, чем в предыдущем, а в последнем ряду 280 мест. Сколько человек вмещает амфитеатр?
Далее...
  Арифметическая прогрессия Арифметическая прогрессия — такая числовая последовательность, каждый член которой равен предыдущему, увеличенному на одинаковое число. Это число является разностью арифметической прогрессии и обозначается буквой d.  В качестве примера рассмотрим следующие последовательности:  1, 12, 23, 34, 45  Найдём первые 10 членов арифметической прогрессии:  An=a1+(n-1)d  A10=1+(10-1)11=100  Следовательно  1, 12, 23, 34, 45, 56, 67, 78, 89, 100
Далее...